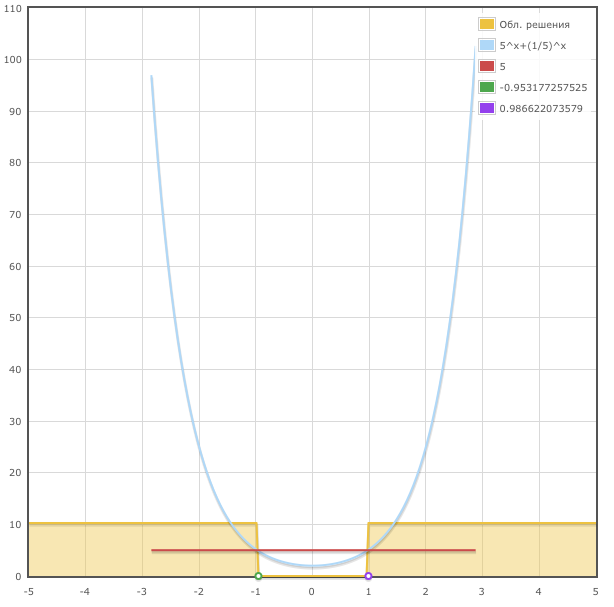
Решим показательное неравенство 5^x + (1/5)^x > 5 с помощью онлайн сервиса, который находится по ссылке
>>решение неравенств онлайн <<
Введём указанное неравенство в данный калькулятор:
Вы получите следующее подробное решение для неравенства:
Дано неравенство: $$5^{x} + \left(\frac{1}{5}\right)^{x} > 5$$ Чтобы решить это нер-во - надо сначала решить соотвествующее ур-ние: $$5^{x} + \left(\frac{1}{5}\right)^{x} = 5$$ Решаем:
Дано уравнение: $$5^{x} + \left(\frac{1}{5}\right)^{x} = 5$$ или $$5^{x} + \left(\frac{1}{5}\right)^{x} - 5 = 0$$ Сделаем замену $$v = \left(\frac{1}{5}\right)^{x}$$ получим $$v - 5 + \frac{1}{v} = 0$$ или $$v - 5 + \frac{1}{v} = 0$$ делаем обратную замену $$\left(\frac{1}{5}\right)^{x} = v$$ или $$x = - \frac{\log{\left (v \right )}}{\log{\left (5 \right )}}$$ $$x_{1} = \frac{1}{\log{\left (5 \right )}} \left(- \log{\left (2 \right )} + \log{\left (\sqrt{21} + 5 \right )}\right)$$ $$x_{2} = \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} - \log{\left (2 \right )}\right)$$ $$x_{1} = \frac{1}{\log{\left (5 \right )}} \left(- \log{\left (2 \right )} + \log{\left (\sqrt{21} + 5 \right )}\right)$$ $$x_{2} = \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} - \log{\left (2 \right )}\right)$$ Данные корни $$x_{2} = \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} - \log{\left (2 \right )}\right)$$ $$x_{1} = \frac{1}{\log{\left (5 \right )}} \left(- \log{\left (2 \right )} + \log{\left (\sqrt{21} + 5 \right )}\right)$$ являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки: $$x_{0} < x_{2}$$ Возьмём например точку $$x_{0} = x_{2} - 1$$ =
/ ____\
-log(2) + log\5 - \/ 21 /
------------------------- - 1
1
log (5)
= $$-1 + \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} - \log{\left (2 \right )}\right)$$ подставляем в выражение $$5^{x} + \left(\frac{1}{5}\right)^{x} > 5$$
/ ____\ / ____\
-log(2) + log\5 - \/ 21 / -log(2) + log\5 - \/ 21 /
------------------------- - 1 - ------------------------- + 1
1 1
log (5) log (5)
5 + 5 > 5
/ ____\ / ____\
-log(2) + log\5 - \/ 21 / -log(2) + log\5 - \/ 21 /
-1 + ------------------------- 1 - ------------------------- > 5
log(5) log(5)
5 + 5
значит одно из решений нашего неравенства будет при:
$$x < \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} - \log{\left (2 \right )}\right)$$
_____ _____
\ /
-------ο-------ο-------
x2 x1
Другие решения неравенства будем получать переходом на следующий полюс
и т.д.
Ответ: $$x < \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} - \log{\left (2 \right )}\right)$$ $$x > \frac{1}{\log{\left (5 \right )}} \left(- \log{\left (2 \right )} + \log{\left (\sqrt{21} + 5 \right )}\right)$$
Также вы будете иметь графическое решение показательного неравенства:
