UPD: Теперь вы можете вводить условия задачи Коши прямо в форму:

Рассмотрим пример решения задачи Коши с помощью онлайн калькулятора "Контрольная-работа.Ру".

Внимание! Следуя этому примеру и подробно и внимательно читая вы сможете решить и свою задачу, просто следуя тем же шагам!

Возьмём задачу из контрольной "Решить задачу Коши для дифференциального уравнения второго порядка":

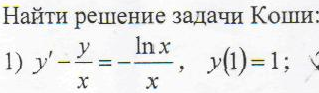
Для того, чтобы решить данную задачу откройте сервис решения дифференциальных уравнений онлайн

и введите в форму левую часть уравнения y' - y/x

а в правую часть уравнения: -lnx/x

как на картинке:

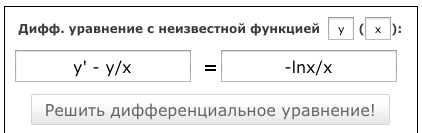
Нажимаем кнопку "Решить дифференциальное уравнение!"

Видим ответ для этого дифф. ур-ния:

y(x) == C1*x + log(x) + 1

Но как вы знаете, это ещё не решение задачи Коши, это всего лишь решение дифференциального уравнения.

Теперь по начальным условиям y(1) = 1 надо найти C1.

Для этого воспользуемся сервисом по решению обычных уравнений онлайн

Вобъём в форму обычных уравнений в правую часть уравнения c*x + log(x) + 1, а в левую y

А также укажем, что уравнение с неизвестной c=C1

На рис. всё это видно:

Нажимаем кнопку "Решить уравнение!"

Получаем ответ для C1

y - log(x) - 1
──────────────
      x       

Но и это ещё не всё.

Надо указать, что y = 1 и x = 1 (т.к. y(1)=1). Подставляем по той же ссылке как на рис. ниже:

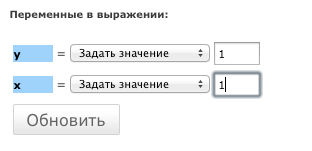
Нажимаем кнопку "Обновить"

И получаем окончательный ответ для C1:

C1 = c = 0

Подставляем это C1 в решение дифф. уравнения и мы получим решение нашей задачи Коши:

y(x) = C1*x + log(x) + 1 = 0*x + log(x) + 1 = log(x) + 1