Иррациональные уравнения бывают от простых до сложных - и всех их можно решить онлайн и с подробным решением с помощью калькулятора онлайн.
Итак:
- Простые иррациональные уравнения
- Иррациональные уравнения средней сложности
- Сложные иррациональные уравнения
Простые иррациональные уравнения
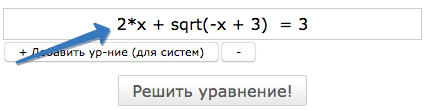
Будем считать, что простые уравнения будут содержат только одну часть иррациональности. Тогда рассмотрим пример:
2*x + sqrt(-x + 3) = 3
Введём это уравнение в форму калькулятора
Тогда, вы получите подробное решение:
Дано уравнение
_______ \/ 3 - x + 2*x = 3
_______ \/ 3 - x = 3 - 2*x
Возведём обе части ур-ния в(о) 2-ую степень
2
3 - x = (3 - 2*x)
2
3 - x = 9 - 12*x + 4*x
Перенесём правую часть уравнения левую часть уравнения со знаком минус
2
-6 - 4*x + 11*x = 0
Это уравнение вида
a*x^2 + b*x + c = 0
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
___
\/ D - b
x1 = ---------
2*a
___
-b - \/ D
x2 = ----------
2*a
где D = b^2 - 4*a*c - это дискриминант.
Т.к.
a = -4
b = 11
c = -6
, то
D = b^2 - 4 * a * c =
(11)^2 - 4 * (-4) * (-6) = 25
Т.к. D > 0, то уравнение имеет два корня.
x1 = (-b + sqrt(D)) / (2*a)
x2 = (-b - sqrt(D)) / (2*a)
или
x1 = 3/4
x2 = 2
Т.к.
_______ \/ 3 - x = 3 - 2*x
и
_______ \/ 3 - x >= 0
то
3 - 2*x >= 0
или
x <= 3/2
-oo < x
Тогда, окончательный ответ:
x1 = 3/4
Средние иррациональные уравнения
Средними же будем считать уравнения, которые содержат две иррациональные части в уравнении.
Например,
sqrt(4*x + 1) + sqrt(3*x - 2) = 2
надо ввести в форму в калькуляторе
Результат будет таким:
Дано уравнение
_________ __________ \/ 1 + 4*x + \/ -2 + 3*x = 2
Возведём обе части ур-ния в(о) 2-ую степень
2
/ _________ __________\
\\/ 1 + 4*x + \/ -2 + 3*x / = 4
или
2 _____________________ 2 1 *(3*x - 2) + 2*\/ (3*x - 2)*(4*x + 1) + 1 *(4*x + 1) = 4
или
__________________
/ 2
-1 + 2*\/ -2 - 5*x + 12*x + 7*x = 4
преобразуем:
__________________
/ 2
2*\/ -2 - 5*x + 12*x = 5 - 7*x
Возведём обе части ур-ния в(о) 2-ую степень
2 2
-8 - 20*x + 48*x = (5 - 7*x)
2 2
-8 - 20*x + 48*x = 25 - 70*x + 49*x
Перенесём правую часть уравнения левую часть уравнения со знаком минус
2
-33 - x + 50*x = 0
Это уравнение вида
a*x^2 + b*x + c = 0
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
___
\/ D - b
x1 = ---------
2*a
___
-b - \/ D
x2 = ----------
2*a
где D = b^2 - 4*a*c - это дискриминант.
Т.к.
a = -1
b = 50
c = -33
, то
D = b^2 - 4 * a * c =
(50)^2 - 4 * (-1) * (-33) = 2368
Т.к. D > 0, то уравнение имеет два корня.
x1 = (-b + sqrt(D)) / (2*a)
x2 = (-b - sqrt(D)) / (2*a)
или
____
x1 = 25 - 4*\/ 37
____
x2 = 25 + 4*\/ 37
Т.к.
__________________
/ 2 5 7*x
\/ -2 - 5*x + 12*x = - - ---
2 2
и
__________________ / 2 \/ -2 - 5*x + 12*x >= 0
то
5 7*x - - --- >= 0 2 2
или
x <= 5/7
-oo < x
____
x1 = 25 - 4*\/ 37
проверяем:
____
x1 = 25 - 4*\/ 37
__________ ___________
-2 + \/ 1 + 4*x1 + \/ -2 + 3*x1 = 0
=
_______________________ ________________________ / / ____\ / / ____\ \/ 1 + 4*\25 - 4*\/ 37 / + \/ -2 + 3*\25 - 4*\/ 37 / - 2 = 0
=
0 = 0
- тождество
Тогда, окончательный ответ:
____
x1 = 25 - 4*\/ 37
Сложные иррациональные уравнения
Самыми сложными же будут уравнения с тремя частями иррациональностями, значит будет такой пример:
sqrt(x + 5) - sqrt(x - 1) = sqrt(2*x + 4)
В форме калькулятора это будет выглядеть так:
Тогда получите подробное объяснение
Дано уравнение
_______ ________ _________ \/ 5 + x - \/ -1 + x = \/ 4 + 2*x
Возведём обе части ур-ния в(о) 2-ую степень
2
/ _______ ________\
\\/ 5 + x - \/ -1 + x / = 4 + 2*x
или
2 _________________ 2 1 *(x + 5) - 2*\/ (x + 5)*(x - 1) + (-1) *(x - 1) = 4 + 2*x
или
_______________
/ 2
4 - 2*\/ -5 + x + 4*x + 2*x = 4 + 2*x
преобразуем:
_______________
/ 2
-2*\/ -5 + x + 4*x = 0
преобразуем
2
-5 + x + 4*x = 0
Это уравнение вида
a*x^2 + b*x + c = 0
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
___
\/ D - b
x1 = ---------
2*a
___
-b - \/ D
x2 = ----------
2*a
где D = b^2 - 4*a*c - это дискриминант.
Т.к.
a = 1
b = 4
c = -5
, то
D = b^2 - 4 * a * c =
(4)^2 - 4 * (1) * (-5) = 36
Т.к. D > 0, то уравнение имеет два корня.
x1 = (-b + sqrt(D)) / (2*a)
x2 = (-b - sqrt(D)) / (2*a)
или
x1 = 1
x2 = -5
проверяем:
x1 = 1
________ _________ __________ \/ 5 + x1 - \/ -1 + x1 - \/ 4 + 2*x1 = 0
=
_______ ________ _______ \/ 5 + 1 - \/ -1 + 1 - \/ 4 + 2 = 0
=
0 = 0
- тождество
x2 = -5
________ _________ __________ \/ 5 + x2 - \/ -1 + x2 - \/ 4 + 2*x2 = 0
=
_______ ________ ____________ \/ 5 - 5 - \/ -1 - 5 - \/ 4 + 2*(-5) = 0
=
-2*i*sqrt(6) = 0
- Нет
Тогда, окончательный ответ:
x1 = 1