Здесь будет приведена инструкция, как не выполняя построения - найти точки пересечения графиков онлайн.

Допустим, даны два графика функции:

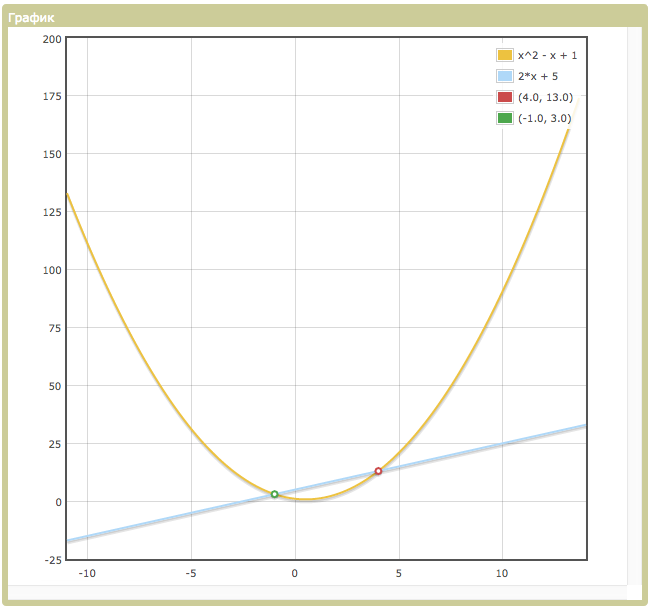
1. Парабола y = f(x) = x^2 - x + 1

2. Прямая y = g(x) = 2*x + 5

Графики будут пересекаться, если f(x) = g(x)

Так вот - надо взять первый график функции - поставить в левую часть уравнения.

Второй график надо поставить в правую часть уравнения.

Получим уравнение:

f(x) = g(x)

x^2 - x + 1 = 2*x + 5

Таким образом, у нас появилась возможность не выполняя построения найти точки пересечения

Калькулятор онлайн сам решит его:

Перенесём правую часть уравнения в левую часть уравнения со знаком минус. Уравнение превратится из $$x^{2} - x + 1 = 2 x + 5$$ в $$- 2 x - 5 + x^{2} - x + 1 = 0$$ Это уравнение вида
a*x^2 + b*x + c = 0
Квадратное уравнение можно решить с помощью дискриминанта.
Корни квадратного уравнения: $$x_{1} = \frac{\sqrt{D} - b}{2 a}$$ $$x_{2} = \frac{- \sqrt{D} - b}{2 a}$$ где D = b^2 - 4*a*c - это дискриминант. Т.к. $$a = 1$$ $$b = -3$$ $$c = -4$$ , то D = b^2 - 4 * a * c = (-3)^2 - 4 * (1) * (-4) = 25.
Т.к. D > 0, то уравнение имеет два корня.
x1 = (-b + sqrt(D)) / (2*a)
x2 = (-b - sqrt(D)) / (2*a)
или $$x_{1} = 4$$ $$x_{2} = -1$$

Проверяем с построением: