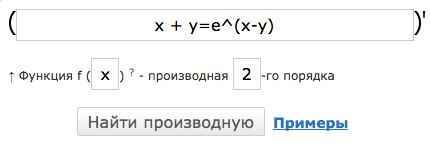
Пусть дана функция:

x + y=e^(x-y)

Введём в форму:

Получим результат:

            x - y(x)
x + y(x) = e        



                 x - y(x)
d          -1 + e        
--(y(x)) = --------------
dx              x - y(x) 
           1 + e         



            /    d       \  x - y(x)   /    d       \ /      x - y(x)\  x - y(x)
  2         |1 - --(y(x))|*e           |1 - --(y(x))|*\-1 + e        /*e        
 d          \    dx      /             \    dx      /                           
---(y(x)) = ------------------------ - -----------------------------------------
  2                   x - y(x)                                     2            
dx               1 + e                              /     x - y(x)\             
                                                    \1 + e        /             

            /          x - y(x)\             /          x - y(x)\                           
            |    -1 + e        |  x - y(x)   |    -1 + e        | /      x - y(x)\  x - y(x)
            |1 - --------------|*e           |1 - --------------|*\-1 + e        /*e        
  2         |         x - y(x) |             |         x - y(x) |                           
 d          \    1 + e         /             \    1 + e         /                           
---(y(x)) = ------------------------------ - -----------------------------------------------
  2                      x - y(x)                                           2               
dx                  1 + e                                    /     x - y(x)\                
                                                             \1 + e        /