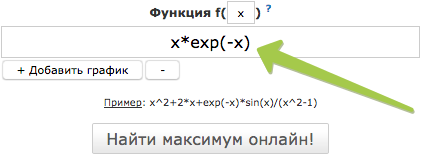
Максимум функции определяется как экстремум функции, но добавляются дополнительные условия.

Воспользуйтесь калькулятором по нахождению максимума функции:

Получим результат:

Максимум равен y=1/e, в точке x=1

Для того, чтобы найти экстремумы, нужно решить уравнение $$\frac{d}{d x} f{\left (x \right )} = 0$$ (производная равна нулю), и корни этого уравнения будут экстремумами данной функции: $$\frac{d}{d x} f{\left (x \right )} = $$ Первая производная $$- x e^{- x} + e^{- x} = 0$$ Решаем это уравнение
Корни этого ур-ния: $$x_{1} = 1$$ Зн. экстремумы в точках:
-1 (1, e )
Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумов у функции нет.
Максимумы функции в точках: $$x_{1} = 1$$ Убывает на промежутках
(-oo, 1]
Возрастает на промежутках
[1, oo)

Определение максимума функции

Максимум функции - это максимальное значение на данном промежутке. Максимум находится так:
Решается уравнение : "Производная функции равна 0" для неизвестной x (если функция зависит от x) и смотрится при найденном x как меняет точка знак производной функции, проходя через эту точку

Другой простой пример максимума функции

Рассмотрим функцию -x^2. Ее производная равна -2*x (Кстати производная функции находится здесь) - решаем уравнение -2*x = 0 - значит x = 0.

Смотрим - производная -2x при x > 0 - меньше 0, а при x < 0 производная больше 0.

Значит при x=0 функция -x^2 имеет максимум. Вот такой простой пример.