Как пользоваться сервисом "Метод Наименьших Квадратов" · Как пользоваться Контрольная Работа РУ

Расскажу, как пользоваться сервисом "Метод наименьших квадратов" онлайн.

Линейная аппроксимация МНК

Допустим вам даны данные эксперимента: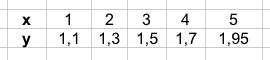 Данные эксперимента для линейной аппроксимации методом наименьших квадратов

и вы хотите произвести линейную аппроксимацию на прямую (нелинейная тут) с доверительной вероятностью p=0,95. Чтобы воспользоваться данным сервисом, нужно подготовить данные эксперимента, а именно перенести эти данные в файл программы excel с расширением xls. Пример файла можно скачать тут. Все, данные подготовлены, нажимаем кнопку "Аппроксимировать". перейти к сервису: >> здесь << Результат для приведенного примера будет таким:

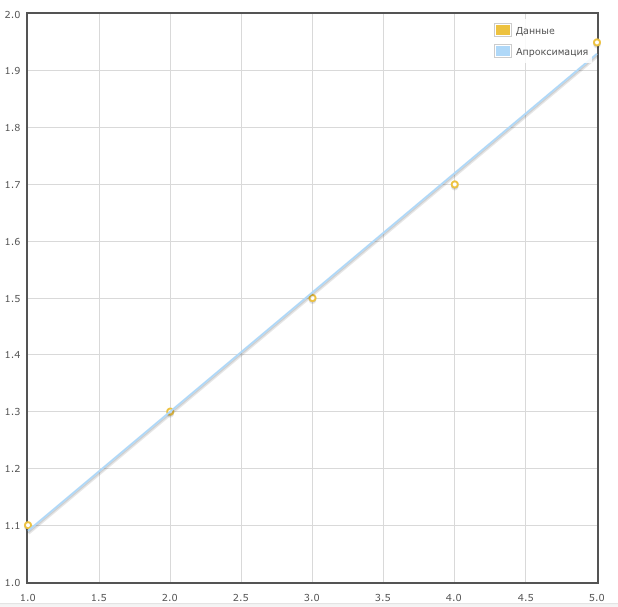
Сделаем линейную аппроксимацию методом наименьших квадратов для данных.
Попытаемся представить данные в виде y = a*x + b.

	x_i	y_i	x_i - x	(x_i - x)²	y_i - y	(x_i - x)(y_i - y)
	1.0	1.1	-2.0	4.0	-0.41	0.82
	2.0	1.3	-1.0	1.0	-0.21	0.21
	3.0	1.5	0.0	0.0	-0.01	0
	4.0	1.7	1.0	1.0	0.19	0.19
	5.0	1.95	2.0	4.0	0.44	0.88
Сумма	15.0	7.55		10.0		2.1

где x = (1.0 + 2.0 + 3.0 + 4.0 + 5.0)/5 = 15.0/ 5 = 3.0,
y = (1.1 + 1.3 + 1.5 + 1.7 + 1.95)/5 = 7.55/ 5 = 1.51,

a = ∑(x_i - x)(y_i - y)/∑(x_i - x)² - суммы i=1 до 5, зн. из таблицы

a = 2.1/10.0 = 0.21 b = y - a*x, значит b = 1.51 - 0.21*3.0 = 0.88 поэтому y = a*x + b = 0.21*x + 0.88

Посчитаем среднеквадратичные ошибки определения a и b:

т.к. S_a² = ∑[(y_i - a*x_i - b)²]/(n - 2)/∑[(x_i - x)²],

то S_a = √0.001/(5 - 2)/10.0 = 0.0057735026919

т.к. S_b² = ∑[(y_i - a*x_i - b)²]/(n - 2)*(1/n + (x)²/∑[(x_i - x)²]),

то S_b = √0.001/(5 - 2)*(1/5 + 3.0²/10.0) = 0.0191485421551

При доверительной вероятности p=0.95: абсолютные ошибки определения a и b:

При такой вероятности p и количестве измерений n=5 кол-во степеней свободы f=4, зн. коэффициент Студьента (таблица) равен t=2.7764451052, тогда:

абсолютные ошибки для a и b:

Δ_a = t*S_a = 2.7764451052*0.0057735026919 = 0.0160298132888
Δ_b = t*S_b = 2.7764451052*0.0191485421551 = 0.0531648761383

Последний знак у a после запятой по счёту - 2й, значит у Δ_a оставляем 3 знаков после запятой

Последний знак у b после запятой по счёту - 2й, значит у Δ_b оставляем 3 знаков после запятой

Поэтому аппроксимация будет выглядеть так:

y = a*x + b, где
a = 0.21 ± 0.016
b = 0.88 ± 0.053;

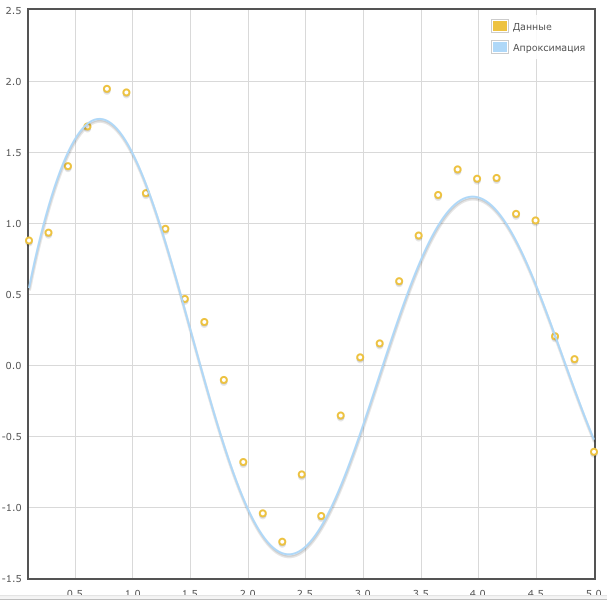
Нелинейная аппроксимация

Есть ещё обобщённый метод наименьших квадратов, который позволяет аппроксимировать до нелинейных функций. Им тоже можно воспользоваться по ссылке >> здесь << только нужно выбрать метод Обобщенный (нелинейный) Если ввести такие данные как эти и указать нелинейную функцию k1/(x^k2)*sin(k3*x), то получиться такой результат:

Найденные аппроксимированные параметры:

k1 = 1.62408905511
k2 = 0.228873651613
k3 = 1.98234923393

Получается график функции:
f(x) = k1/(x^k2)*sin(k3*x) = 1.62408905511498*x^(-0.228873651613201)*sin(1.98234923393379*x)

А график с нелинейной аппроксимацией будет