Примеры

$$9 x^{2} + 12 x y - 24 x + 4 y^{2} - 16 y + 3 = 0$$

$$x^{2} - 2 x y - 10 x + y^{2} - 6 y + 25 = 0$$

$$5 x^{2} + 4 x y - 6 x + y^{2} - 2 y + 2 = 0$$

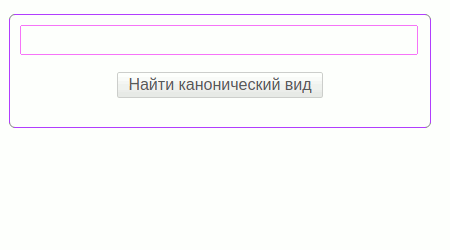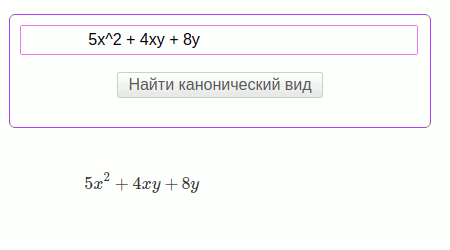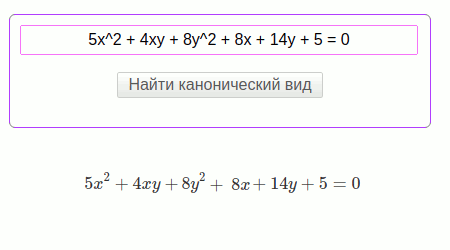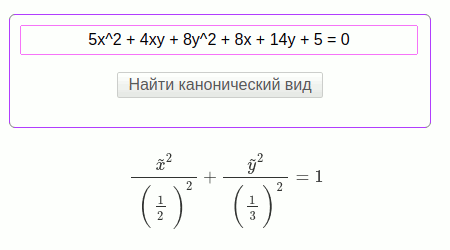
$$5 x^{2} + 4 x y + 8 x + 8 y^{2} + 14 y + 5 = 0$$

$$2 x^{2} - 4 x y + 4 y^{2} - 4 y + z^{2} - 2 z + 5 = 0$$

$$x^{2} - 2 x + y^{2} - 2 y - z^{2} + 2 z + 2 = 0$$

$$x^{2} - 6 x + y^{2} + 6 y - 4 z + 18 = 0$$

$$x^{2} + 4 x y + 6 x z - 4 x + 4 y^{2} + 12 y z - 8 y + 9 z^{2} - 12 z + 3 = 0$$

Про калькулятор канонического вида

1. По заданному уравнению находит:

Канонический вид уравнения (для линий и поверхностей второго порядка)

Базис-вектора канонической системы координат (для линий 2-го порядка)

Центр канонической системы координат (для линий 2-го порядка)

2. Подробное решение двумя способами:

Прямой метод с переходом к новому центру координат и вращению вокруг нового центра координат (для линий)

Метод инвариантов с вычислением множества детерминантов (для линий и поверхностей)

3. Еще:

Строит график линии второго порядка, построение центра канонической системы и построение базисных векторов канонической системы